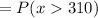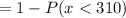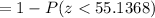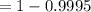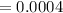Question

An airline company is considering a new policy of booking as many as 318 persons on an airplane that can seat only 310. (Past studies have revealed that only 90% of the booked passengers actually arrive for the flight.) Estimate the probability that if the company books 318 persons. not enough seats will be available.

Answer 1

Hence, the required probability is
`0.0004`.

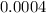Given :

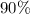`90\%` of the booked passengers arrive for the flight.

Number of booked passengers n
`=318`

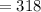
Number of seats available x
`=310`

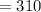
To find :

The probability that if the company books 318 persons.

Explanation :

`n=318,x=310`

`P=0.09(90\%)`

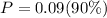
Mean
`\bar{x}=nP`

`\Rightarrow \bar{x}=318* 0.09`

`\Rightarrow \bar{x}=28.62`

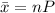
Standard deviation
`\sigma =\sqrt{nPq` where
`q=1-P`

`\Rightarrow \sigma =√(318* 0.09* 0.91)`

`\Rightarrow \sigma=√(26.0442)`

`\Rightarrow \sigma =5.1033`

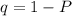
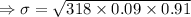
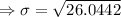
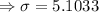
Required probability
`=P(x>310)`

`=1-P(x<310)`

`=1-P(\frac{x-\bar{x}}{\sigma}<(310-28.62)/(5.1033))`

`=1-P(z<55.1368)`

`=1-0.9995`

`=0.0004`