What is the equation of the line that passes through the points (4,3),(6,5)?

Question

asked May 14, 2023 22.9k views

2 Answers

Isaac Muturi · Answer 1 · 2023-05-17T09:04:47+0000

Answer:

y=x-1

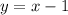
Skills needed: Point-slope Form

Explanation:

1) First, let's try to make sense out of the problem. We are given two coordinate points and have to create a line out of it.

---> The most efficient way to solve this is with point-slope form.

The point slope form, given One coordinate point and Slope is:

Given coordinate pair
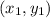(x_1, y_1) and Slope

--->
y-y_1=m(x-x_1)

2) Now, we have one coordinate pair/point, but we need slope.

---> The slope is the rate of change, and can be found with a formula:

Given two coordinate points
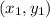(x_1,y_1) and
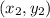(x_2, y_2) , the slope is:

--->
(y_2-y_1)/(x_2-x_1)

Let's use this formula for the points above:

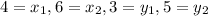
4=x_1, 6=x_2, 3=y_1, 5=y_2

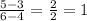
(5-3)/(6-4) = (2)/(2) = 1

Based on the above: Slope = 1 (or
m=1 )

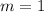3) Next, we use point slope form. Let's use coordinate pair (4, 3) -- It does not matter which one:

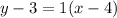
y-3=1(x-4)

The 1 does not mean anything (since anything multiplied by 1 is itself, so it can be taken out:

y-3=x-4

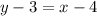
Now to get it to slope-intercept form (
y=mx+b ) ---> We add 3 to both sides

--->
$y-3+3=x-4+3 \\ y=x-1$

y=x-1 is the final equation.