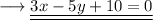Answer:
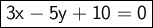
Explanation:
A equation is given to us and we need to find out the equation of the line which is perpendicular to the given line and passes through (-20,-10). The given line is ,
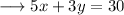
Convert this into slope intercept form of the line , which is y = mx + c.
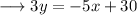
Divide both sides by 3,
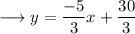
Simplify ,
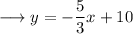
On comparing it to slope intercept form, we have ;
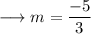
Now as we know that the product of slopes of two perpendicular lines is -1 . Therefore the slope of the perpendicular line will be negative reciprocal of the slope of first line. As ,
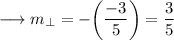
Now we may use the point slope form of the line which is ,
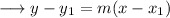
Substitute the respective values ,
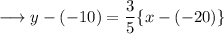
Simplify the brackets ,
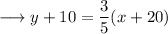
Cross multiply ,
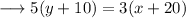
Distribute ,
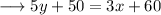
Subtract (5y +50) to both sides ,
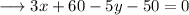
Simplify ,