Question

Find the geometric mean between 6 and 48 given the sequence (3,6,12,24,48,96)

Answer 1

16.97

Explanation:

the geometric mean value of a set of n numbers is the nth root of the product of all n numbers.

so, here this means

`gm = \sqrt[6]{3 * 6 * 12 * 24 * 48 * 96}`

this would be 16.97

but careful, the problem only asks for the gm between 6 and 48 of the sequence.

so, we actually only consider the subset 6, 12, 24, 48.

therefore

`gm = \sqrt[4]{6 * 12 * 24 * 48}`

this is also

`gm = \sqrt[4]{3 * 2 * 3 * 2 * 2 * 3 * 2 * 2 * 2 * 3 * 2 * 2 * 2 * 2}`

`= \sqrt[4]{ {3}^(4) * {2}^(10) }`

`= \sqrt[4]{ {3}^(4) * {2}^(4) * {2}^(4) * {2}^(2) }`

`= 3 * 2 * 2 * \sqrt[4]{ {2}^(2) }`

`= 12 * √(2)`

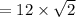
so, we could specify the result as that simple expression

or calculate it

gm = 16.97

hey, the result is the same as for the complete sequence.

coincidence ? no, it is not. but that is a subject for a different question.