Answer:
Do you want to be extremely boring?
Since the value is 2 at both 0 and 1, why not make it so the value is 2 everywhere else?
 is a valid solution.
is a valid solution.
Want something more fun? Why not a parabola?
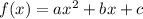 .
.
At this point you have three parameters to play with, and from the fact that
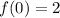 we can already fix one of them, in particular
we can already fix one of them, in particular
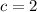 . At this point I would recommend picking an easy value for one of the two, let's say
. At this point I would recommend picking an easy value for one of the two, let's say
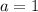 (or even
(or even
 , it will just flip everything upside down) and find out b accordingly:
, it will just flip everything upside down) and find out b accordingly:
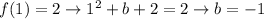
Our function becomes
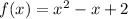
Notice that it works even by switching sign in the first two terms:
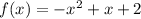
Want something even more creative? Try playing with a cosine tweaking it's amplitude and frequency so that it's period goes to 1 and it's amplitude gets to 2:
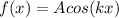
Since cosine is bound between -1 and 1, in order to reach the maximum at 2 we need
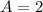 , and at that point the first condition is guaranteed; using the second to find k we get
, and at that point the first condition is guaranteed; using the second to find k we get

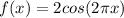
Or how about a sine wave that oscillates around 2? with a similar reasoning you get
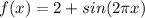
Sky is the limit.