Question

A simple random sample of 6,250 history majors at U.S. universitites was taken. Almost all of them could correctly name Abraham Lincoln's second Vice President, but only 11.3% of them knew his first Vice President. If possible, find a 95%-confidence interval for the percentage of history majors at U.S. universities who knew Abraham Lincoln's first Vice President. If this is not possible, why not

Answer 1

The 95%-confidence interval for the percentage of history majors at U.S. universities who knew Abraham Lincoln's first Vice President is (10.5%, 12.1%).

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the z-score that has a p-value of
`1 - (\alpha)/(2)`.

6250 students, 11.3% knew Abraham Lincoln's first vice-president.

This means that
`n = 6250, \pi = 0.113`

95% confidence level

So
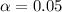`\alpha = 0.05`, z is the value of Z that has a p-value of
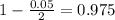`1 - (0.05)/(2) = 0.975`, so
`Z = 1.96`.

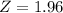The lower limit of this interval is:

`\pi - z\sqrt{(\pi(1-\pi))/(n)} = 0.113 - 1.96\sqrt{(0.113*0.887)/(6250)} = 0.105`

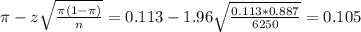
The upper limit of this interval is:

`\pi + z\sqrt{(\pi(1-\pi))/(n)} = 0.113 + 1.96\sqrt{(0.113*0.887)/(6250)} = 0.121`

As percentages:

0.105*100% = 10.5%

0.121*100% = 12.1%

The 95%-confidence interval for the percentage of history majors at U.S. universities who knew Abraham Lincoln's first Vice President is (10.5%, 12.1%).