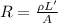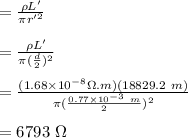Question

To demonstrate the large size of the henry unit, a physics professor wants to wind an air-filled solenoid with self-inductance of 1.0 HH on the outside of a 15 cmcm diameter plastic hollow tube using copper wire with a 0.93 mmmm diameter. The solenoid is to be tightly wound with each turn touching its neighbor (the wire has a thin insulating layer on its surface so the neighboring turns are not in electrical contact).

Required:
a. How long will the plastic tube need to be?
b. How many kilometers of copper wire will be required?
c. What will be the resistance of this solenoid?

Answer 1

Following are the solution to the given points:

Step-by-step explanation:

For point a:

Following are the expression to the self- inductance and the solenoid:

`L=(\mu_0 N^2 A)/(l)`

`=(\mu_0 ((l)/(d))^2 (\pi r^2))/(l)\\\\=(\mu_0 ( \pi((D)/(2))^2))/(d^2)\\\\=(Ld^2)/(\mu_0( \pi ((D)/(2))^2))\\\\=((1.0 \ H)(0.77 * 10^(-3) \ m)^2)/( 4 \pi * 10^(-7) (H)/(m) (\pi ((13 * 10^(-2) \ m )/(2))^2))\\\\=35.5 \ m`

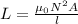
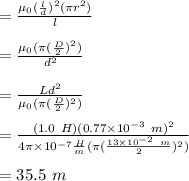
For point b:

Calculting the length of the copper wire:

`L'=N(\pi D)`

`=(l)/(d)(\pi D)\\\\=(35.5 m)/(0.77 * 10^(-3) m)\pi (13* 10^(-2) m)\\\\=18829.2 \ m((1 km)/(10^3 \ m))\\\\=18.8 \ km`

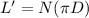
For point c:

The resistance of the solenoid is given by,

`R=(\rho L')/(A)`

`=(\rho L')/(\pi r'^2)\\\\=(\rho L')/(\pi ((d)/(2))^2)\\\\=((1.68* 10^(-8) \Omega . m) (18829.2 \ m))/(\pi ((0.77 * 10^(-3) \ m)/(2))^2)\\\\=6793 \ \Omega`