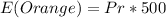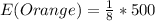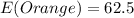Question

ANSWER IT HOW THE QUESTIONS ARE ASKED!! Thank you so much!!

Answer 1

`(a)\ Pr = (2)/(5)`

`(b)\ Pr = (9)/(20)`

`(c)\ E(Orange) = 100`

`(d)\ E(Orange) = 62.5`

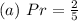
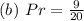
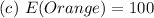
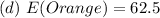
Explanation:

Solving (a): Theoretical probability of green or yellow

Here, we consider the spinner itself

From the attached image, we have:

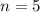`n= 5` --- i.e. 5 sections

`Yellow = 1`

`Green = 1`

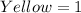
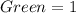
So, the probability is:

`Pr = P(Yellow)\ or\ P(Green)`

`Pr = (Yellow)/(n) + (Green)/(n)`

`Pr = (1)/(5) + (1)/(5)`

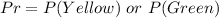
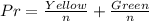
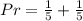
Take LCM

`Pr = (1+1)/(5)`

`Pr = (2)/(5)`

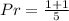
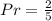
Solving (b): Experimental probability of green or yellow

Here, we consider the result of the experiment

From the attached image, we have:

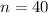`n= 40` --- i.e. 40 spins

`Yellow = 12`

`Green = 6`

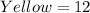
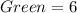
So, the probability is:

`Pr = P(Yellow)\ or\ P(Green)`

`Pr = (Yellow)/(n) + (Green)/(n)`

`Pr = (12)/(40) + (6)/(40)`

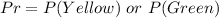
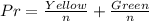
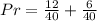
Take LCM

`Pr = (12+6)/(40)`

`Pr = (18)/(40)`

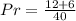
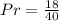
Simplify

`Pr = (9)/(20)`

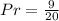
Solving (c): Expectation of orange outcomes in a spin of 500 times, theoretically.

Here, we consider the spinner itself

From the attached image, we have:

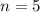`n= 5` --- i.e. 5 sections

`Orange = 1`

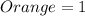
So, the probability of having an outcome of orange in 1 spin is:

`Pr = P(Orange)`

`Pr = (Orange)/(n)`

`Pr = (1)/(5)`

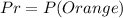
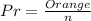
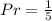
In 500 spins, the expectation is:

`E(Orange) = Pr * 500`

`E(Orange) = (1)/(5) * 500`

`E(Orange) = 100`

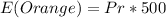
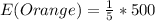
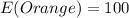
Solving (c): Expectation of orange outcomes in a spin of 500 times, base on experiments.

Here, we consider the spinner itself

From the attached image, we have:

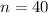`n= 40` --- i.e. 40 spins

`Orange = 5`

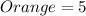
So, the probability of having an outcome of orange is:

`Pr = P(Orange)`

`Pr = (Orange)/(n)`

`Pr = (5)/(40)`

`Pr = (1)/(8)`

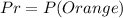
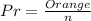
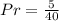
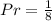
In 500 spins, the expectation is:

`E(Orange) = Pr * 500`

`E(Orange) = (1)/(8) * 500`

`E(Orange) = 62.5`