So, its more like this:
Using the polar form, a complex number with modulus r and argument θ may be written
z = r(cos 0 + j sin θ)
It follows immediately from Euler’s relations that we can also write this complex number in
exponential form as :
z =
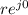
When using this form you should ensure that all angles are measured in radians and not degrees.
The exponential form of a complex number is in widespread use in engineering and science. Since z = r(cosθ + isinθ) and since eiθ = cosθ + isinθ we therefore obtain another way in which to denote a complex number: z = reiθ, called the exponential form.
I'm leaning towards the answer choices A. and C.
But I'm sure it's A because of the two, C has an x. That's the only difference they have.
Here's another example,
Let z=x+iy, its exponential form comes from identifying it as the point (x,y) in the (Argand) plane. This basically amounts to writing it in what would be polar form in the real plane. Writing it as:
z =reiθ
. If you graph the point (x,y) and treat it as a vector its easy to see that r=|z| and θ=tan−1(yx).
For purely real numbers, they are already in exponential form since they are equal to their modulus and θ=0.
Also, you can write:
Re(z)=z+z¯2
if you want to write it purely in terms of z. Both of your numbers are purely real and thus they are already in exponential form. I suppose if you wanted to be strict about it you could write it as:
|1−z|=|1−z|e0i