Answer:
horizontal asymptote at y = 2, vertical asymptote at x = 1
Explanation:
We are given the following function:
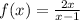
Horizontal asymptote:
The horizontal asymptote of a function is the limit of the function as the input, in this case x, goes to infinity. When we want to find the limit of x going to infinity of a fraction we consider the term with the largest exponent on both the numeration and the denominator. So
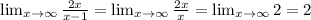
So there is a horizontal asymptote at y = 2
Vertical asymptote:
Vertical asymptotes happens at points outside the function domain.
In this question, we have a fraction, in which the denominator cannot be 0. So
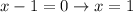
Thus, there is a vertical asymptote at x = 1.
The correct option is:
horizontal asymptote at y = 2, vertical asymptote at x = 1