Question

Find the domain of the rational function.

C(x) = x+9/X^2 -16

Answer 1

Domain = {x : x ≠ 4 , -4} or (-∞ , -4) ∪ (-4 , 4) ∪ (4 , ∞)

Explanation:

TO FIND :-

• Domain of
  `C(x) = (x + 9)/(x^2 - 16)`

SOLUTION :-

Domain of a function is a value for which the function is valid.

The function
`C(x) = (x + 9)/(x^2 - 16)` is valid until the denominator is 0.

So make sure that the denominator must not be 0.

`=> x^2 - 16 > 0`

Find the values of x for which the denominator becomes 0. To find it , you'll have to solve the above inequality.

• Add 16 to both the sides

`=>x^2 - 16 + 16 > 0 + 16`

`=> x^2 > 16`

`=> x > √(16)`

`=> \boxed{x > 4} \: or \:\boxed{x > -4}`

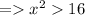
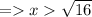
We can say that 4 & -4 can't be domains because these values will make the function undefined.

Now try putting values of x such that -4 < x < 4. You'll observe that the function will be valid for all those values of x between -4 & 4.

CONCLUSION :-

The function will be valid for any value of 'x' except 4 & -4. So in :-

Interval notation , it can be written as → (-∞ , -4) ∪ (-4 , 4) ∪ (4 , ∞)

Set builder notation , it can be written as → {x : x ≠ 4 , -4}