Question

10. RECREATION In a game of kickball, Rickie has to kick the

ball through a semicircular goal to score. If m XZ = 58 and
the m XY = 122, at what angle must Rickie kick the ball to
score? Explain.

Answer 1

The angle Rick must kick the ball to score is an angle between the lines BX and BZY which is less than or equal to 32°

Explanation:

The given measures of the of the angle formed by the tangent to the given circle at X and the secant passing through the circle at Z and Y are;

`m\widehat{XZ} = 58^(\circ)`

`m\widehat{XY} = 122^(\circ)`

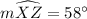
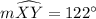
The direction Rick must kick the ball to score is therefore, between the lines BX and BXY

The angle between the lines BX and BXY = ∠XBZ = ∠XBY

The goal is an angle between
`m\widehat{XY}`

Let 'θ' represent the angle Rick must kick the ball to score

Therefore the angle Rick must kick the ball to score is an angle less than or equal to ∠XBZ = ∠XBY

By the Angle Outside the Circle Theorem, we have;

The angle formed outside the circle = (1/2) × The difference of the arcs intercepted by the tangent and the secant

`\therefore \angle XBZ = (1)/(2) * \left (m\widehat{XY} -m\widehat{XZ} \right)`

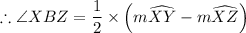
We get;

∠XBZ = (1/2) × (122° - 58°) = 32°

The angle Rick must kick the ball to score, θ = ∠XBZ ≤ 32°