Question

Inside a semicircular tunnel of diameter 30 feet, a vertical support beam is placed 6 feet from the side of the tunnel. How tall is the beam?

Answer 1

The height of the beam is:
`h=12\: feet`

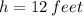
Explanation:

The radius of the tunnel is r = 15 feet

The distance of the beam from the center of the tunnel is:

`d_(beam)=15-6=9\: feet`

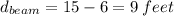
We have a right triangle, where:

• The Hypotenuse is 15 feet
• One side is 9 feet
• The other side is the height of the beam

Let's use Pythagoras theorem.

`15^(2)=9^(2)+h^(2)`

`h^(2)=15^(2)-9^(2)`

`h=\sqrt{15^(2)-9^(2)}`

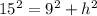
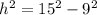
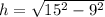
Therefore, the heigh of the beam is:

`h=12\: feet`

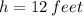
I hope it helps you!