Question

The resistance to motion of a good bicycle on smooth pavement is nearly all due to

aerodynamic drag. Assume that the total mass of rider and bike is M = 100 kg. The frontal area measured from a photograph is A = 0.46 m2. Experiments on a hill, where the road grade is 8 percent, show that terminal speed is Vt = 15 m/s. From these data, drag coefficient is estimated as CD = 1.2.
a) Verify this calculation of drag coefficient.
b) Estimate the distance needed for the bike and rider to decelerate from 15 to 10 m/s while coasting after reaching level road.

Answer 1

The road gradient is given as = tan θ = 0.08

So, θ = 457 degrees, sin θ = 0.08

a). While moving downhill, the terminal velocity the forward force which acts due to the gravitation = backward force due to drag

`$Mg\sin \theta = C_d * (1)/(2) \rho AV^2$`

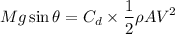
Taking the air density,
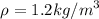`$\rho = 1.2 kg/m^3$` and putting the values we get

`$100 * 9.8 * 0.08 = C_d * (1)/(2) * 1.2 * 0.46 * 15^2$`

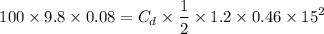
Therefore,
`$C_d = 1.26$`

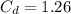
This is approximately the same as the value of coefficient of drag given in the question.

Hence verified.

b). Drag force on level road, F =
`$C_d * (1)/(2)\rho A V^2$`

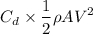
Hence, deceleration :

`$F/m = C_d * (1)/(2m) \rho AV^2$`

`$dV/dt = C_d * (1)/(2m) \rho AV^2$`

`$(dV/ds)(ds/dt) = C_d * (1)/(2m) * \rho AV^2$`

`$V(dV/ds) = C_d * (1)/(2m) * \rho AV^2$`

`$ dV/V= C_d * (1)/(2m) * \rho A * ds$`

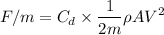
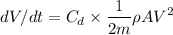
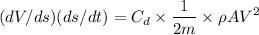
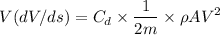
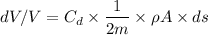
Integrating both the sides, we get

`$\ln (V_2/V_1) = C_d * (1)/(2m) * \rho A * (s_2-s_1)$`

Hence,
`$s_2-s_1 = (2m)/(C_d) * \ln (V_2/V_1) / \rho A$`

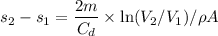
Putting the values,

Distance =
`$2 * (100)/(1.2) * ( \ln(10/15))/((1.2 * 0.46))$`

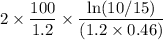
= -122.5 m

Therefore, ignoring the negative sign, we get distance = 122.5 m