Question

A system has two identical components, and requires both the components for system success. If one component fails, the other cannot fail while the failed component is being repaired. The component failure rates and repair rates are 0.1 failures/year and 365 repairs/year respectively. If a similar component is carried as a spare with an average installation time of 1 hour, evaluate the probability of failure, frequency of failure and the average down time of the system.

Answer 1

Explanation:

We are given that:

The failure rate = 0.1 failure/year

i.e. =
`(0.1)/(365* 24)= 0.00001 \ failure /hour`

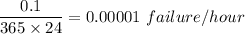
The repair rate = 365 repair/year, if we convert this to repair/hour; we get:

`= (365)/(365* 24) \\ \\ = 0.04 \ repair/ hour`

Time (t) = 1 hour

P(failure) = 1 - R ; if (t=1)

where:

`Reliability (R ) = e^(-\lambda t)(1+ \lambda t) \\ \\ = e^(-0.00001*1)(1+0.00001 *1) \\ \\ \simeq 0.9999`

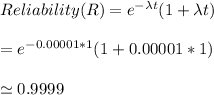
P (failure) = 1 - R

= 1 - 0.9999

= 0.0001

≅ 0

The frequency meantime of failure =
`(1)/(\lambda)`

`(1)/(0.00001)`

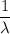
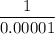
= 100000

The average downtime of repair for the system =
`(1)/(\mu)`

`=(1)/(0.04)`

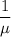
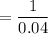
= 25