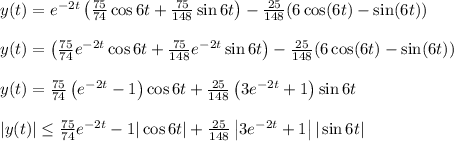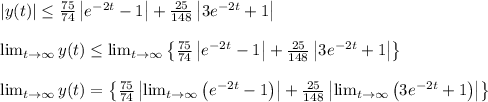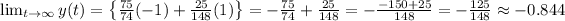Answer:
Hence, the
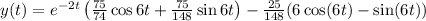 and approximately value of
and approximately value of
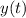 is
is
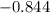 .
.
Given :
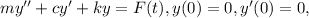
Where
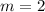 kilograms
kilograms
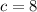 kilograms per second
kilograms per second
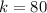 Newtons per meter
Newtons per meter
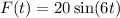 Newtons
Newtons
Explanation :
(1)
Solve the initial value problem.
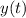
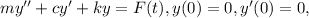
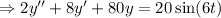
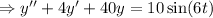
Auxilary equations :
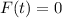
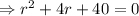
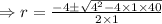
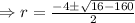
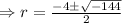
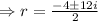

The complementary solution is
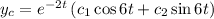
The particular Integral,
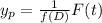

Hence the general solution is :
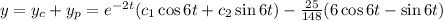
Now we use given initial condition.
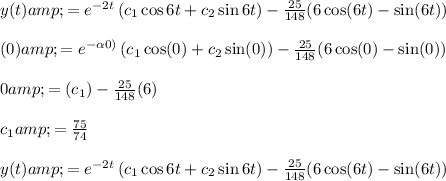
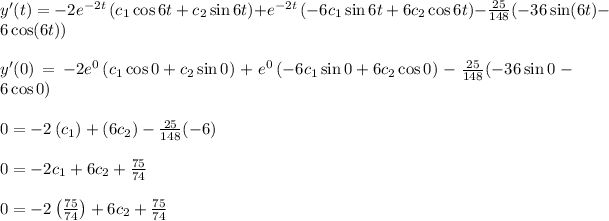
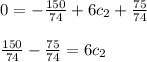
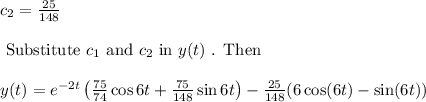
(2)