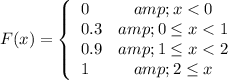Answer:
Hence, the list ten different possible outcomes are
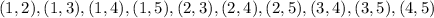 , the probability distribution of X are
, the probability distribution of X are
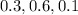 and the cumulative distribution function is
and the cumulative distribution function is
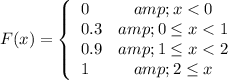
Explanation:
(a)
List the ten different possible outcomes.
The number of ways that two boards are drawn from each lot of
 lots are
lots are
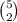
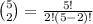
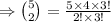
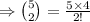

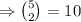
So, the
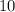 combinations are as follows :
combinations are as follows :
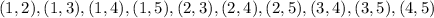
(b)
The aim is to find the probability distribution when two boards are chosen at random and board's one and two is the only defective boards.
Let X be the number of defective boards in the lot.
Therefore, select the combinations of the boards that are without 1 and 2 from 10 combinations.
Compute the
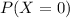
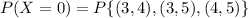

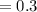
The probability that defectives did not occur in the lot is 0.3
Compute the
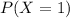
Select the combinations of the boards that are with one defective either 1 and 2 from the 10 combinations.
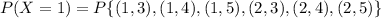
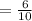
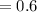
The probability that one defectives occurred in the lot is 0.6.
Compute the
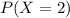
Select the combinations of the boards that are with two defective 1 and 2 from the 10 combinations.
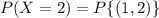
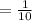
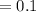
The probability that two defectives occurred in the lot is 0.1.
(c)
The cumulative distribution function (cdf)
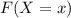 is defined as,
is defined as,
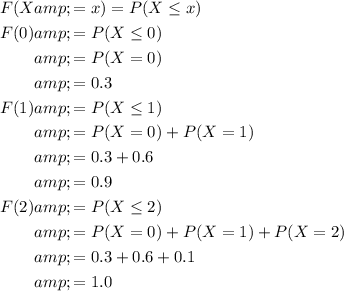
Therefore, the cumulative distribution function (cdf)
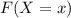 is,
is,