The complete question is as follows: The equilibrium constant, Kp, for the following reaction is 10.5 at 350 K: 2CH2Cl2(g) CH4(g) + CCl4(g) Calculate the equilibrium partial pressures of all species when CH2Cl2(g) is introduced into an evacuated flask at a pressure of 0.968 atm at 350 K. PCH2Cl2 = atm PCH4 = atm PCCl4 = atm
Answer: The equilibrium partial pressures of all species, that is,
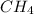 ,
,
 and
and
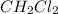 is 0.420 atm, 0.420 atm and 0.128 atm.
is 0.420 atm, 0.420 atm and 0.128 atm.
Step-by-step explanation:
For the given reaction equation, the initial and equilibrium concentration of involved species is as follows.
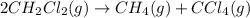
Initial: 0.968 atm 0 0
Equilibrium: (0.968 - 2x) x x
Now,
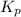 for this reaction is as follows.
for this reaction is as follows.
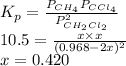
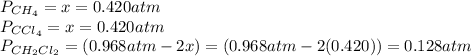
Thus, we can conclude that the equilibrium partial pressures of all species, that is,
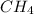 ,
,
 and
and
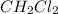 is 0.420 atm, 0.420 atm and 0.128 atm.
is 0.420 atm, 0.420 atm and 0.128 atm.