Answer:
The size of the sample 'n' = 2401
Explanation:
Step:1
Given that the margin of error = 2 % = 0.02
The margin of error is determined by

we know that the proportion
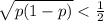
Step:2
The margin of error is determined by
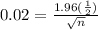
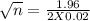
√n = 49
Squaring on both sides, we get
n = 49 × 49
n = 2401
Final answer:-
The size of the sample 'n' = 2401