Question

A cylindrical space colony 8.00 km in diameter and 30.0 km long has been proposed as living quarters for future space explorers. Such a habitat would have cities, land, and lakes on the inside surface and air and clouds in the center. All this would be held in place by the rotation of the cylinder about the long axis. How fast would such a cylinder have to rotate to produce a 1-g gravitational field at the walls of the cylinder

Answer 1

ω = 0.05 rad/s

Step-by-step explanation:

In order to produce the acceleration equal to the acceleration due to gravity at the surface of Earth, the centripetal acceleration must be equal to the value of g:

`a_c = g\\g = (v^2)/(r)\\\\but,\ v=r\omega\\therefore,\\\\g = \omega^2r\\\\\omega = \sqrt{(g)/(r)}`

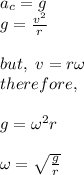
where,

ω = angular speed = ?

g = acceleration due to gravity on the surface of the Earth = 9.81 m/s²

r = radius of cylinder = 8 km/2 = 4 km = 4000 m

Therefore,

`\omega = \sqrt{(9.81\ m/s^2)/(4000\ m)}`

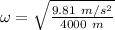
ω = 0.05 rad/s