Answer:
Hence, the expected value of the distance north from city centre archaeologists will have to travel to find the temple is
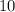 miles and the standard deviation of that distance is
miles and the standard deviation of that distance is
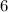 miles.
miles.
Explanation:
Given :
Moment generating function.
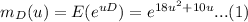
Any two functions can not have the same moment generating function.
The general moment generating function is :
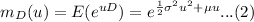
(a)
Now, compare the equation
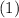 and
and
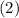 we get,
we get,
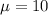
Therefore, the expected value of the distance north from city centre archaeologists will have to travel to find the temple is
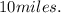
(b)
Now, compare the equation
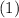 and
and
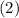 we get,
we get,
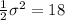
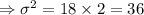
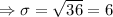
Therefore, the standard deviation of that distance is
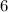 miles.
miles.