Answer:
Yes, The pole will fit through the door because the diagonal width of the door is 10.8 feet, which is longer than the length of the pole.
Explanation:
Using the Pythagorean Theorem, (
 ) we can measure the hypotenuse of a right triangle. Since the doorway is a rectangle, and a rectangle cut diagonally is a right triangle, we can use Pythagorean Theorem to measure the diagonal width of the doorway.
) we can measure the hypotenuse of a right triangle. Since the doorway is a rectangle, and a rectangle cut diagonally is a right triangle, we can use Pythagorean Theorem to measure the diagonal width of the doorway.
Plug in the values of the length and width of the door for a and b. The c value will represent the diagonal width of the doorway:
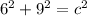
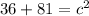
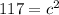
Since 117 is equal to the value of c multiplied by c, we must find the square root of 117 to find the value of c.

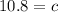
Yes, The pole will fit through the door because the diagonal width of the door is 10.8 feet, which is longer than the length of the pole, measuring 10 feet.