Question

Recall that Rn denotes the right-endpoint approximation using n rectangles, Ln denotes the left-endpoint approximation using n rectangles. Calculate the approximation for each of the given function and interval below. (You may use calculator and keep the final numerical answer in decimals for this question) (a) (3 pts) R5, f(x) = x 2 + x on the interval [−1, 1]

Answer 1

`R_5=1.12`

Explanation:

We want to calculate the right-endpoint approximation (the right Riemann sum) for the function:

`f(x)=x^2+x`

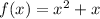
On the interval [-1, 1] using five equal rectangles.

Find the width of each rectangle:

`\displaystyle \Delta x=(1-(-1))/(5)=(2)/(5)`

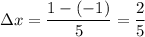
List the x-coordinates starting with -1 and ending with 1 with increments of 2/5:

-1, -3/5, -1/5, 1/5, 3/5, 1.

Since we are find the right-hand approximation, we use the five coordinates on the right.

Evaluate the function for each value. This is shown in the table below.

Each area of each rectangle is its area (the y-value) times its width, which is a constant 2/5. Hence, the approximation for the area under the curve of the function f(x) over the interval [-1, 1] using five equal rectangles is:

`\displaystyle R_5=(2)/(5)\left(-0.24+-0.16+0.24+0.96+2)= 1.12`