Question

Suppose an unknown radioactive substance produces 8000 counts per minute on a Geiger counter at a certain time, and only 500 counts per minute 13 days later. Assuming that the amount of radioactive substance is proportional to the number of counts per minute, determine the half-life of the radioactive substance.

Answer 1

The half-life of the radioactive substance is of 3.25 days.

Explanation:

The amount of radioactive substance is proportional to the number of counts per minute:

This means that the amount is given by the following differential equation:

`(dQ)/(dt) = -kQ`

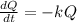
In which k is the decay rate.

The solution is:

`Q(t) = Q(0)e^(-kt)`

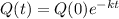
In which Q(0) is the initial amount:

8000 counts per minute on a Geiger counter at a certain time

This means that
`Q(0) = 8000`

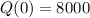
500 counts per minute 13 days later.

This means that
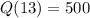`Q(13) = 500`. We use this to find k.

`Q(t) = Q(0)e^(-kt)`

`500 = 8000e^(-13k)`

`e^(-13k) = (500)/(8000)`

`\ln{e^(-13k)} = \ln{(500)/(8000)}`

`-13k = \ln{(500)/(8000)}`

`k = -\frac{\ln{(500)/(8000)}}{13}`

`k = 0.2133`

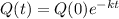
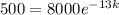
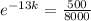
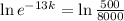
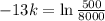
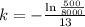
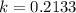
So

`Q(t) = Q(0)e^(-0.2133t)`

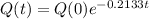
Determine the half-life of the radioactive substance.

This is t for which Q(t) = 0.5Q(0). So

`Q(t) = Q(0)e^(-0.2133t)`

`0.5Q(0) = Q(0)e^(-0.2133t)`

`e^(-0.2133t) = 0.5`

`\ln{e^(-0.2133t)} = ln(0.5)`

`-0.2133t = ln(0.5)`

`t = -(ln(0.5))/(0.2133)`

`t = 3.25`

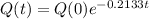
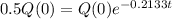
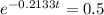
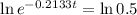
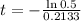
The half-life of the radioactive substance is of 3.25 days.