Answer:
The p-value of the test is 0.0062 < 0.05, which means that this is sufficient evidence that students are using more than just reading comprehension to answer this question
Explanation:
The investigators reasoned that if questions were measuring knowledge or memory rather than just RC, students would answer questions at a higher rate than chance (20%, since there were 5 choices for each question).
This means that at the null hypothesis, we test that the proportion is the probability of answering correctly by change, that is 20%. So
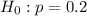
At the alternate hypothesis, we test that the proportion is above 20%, that is:

The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
0.2 is tested at the null hypothesis:
This means that
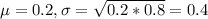
Suppose that on one question, 30 out of 100 examinees answered the question correctly.
This means that

Test statistic:

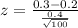
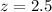
P-value of the test and decision:
The p-value of the test is the probability of finding a sample proportion above 0.3, which is 1 subtracted by the p-value of z = 2.5.
Looking at the z-table, z = 2.5 has a p-value of 0.9938
1 - 0.9938 = 0.0062
The p-value of the test is 0.0062 < 0.05, which means that this is sufficient evidence that students are using more than just reading comprehension to answer this question