Question

It has been observed that some persons who suffer acute heartburn, again suffer acute heartburn within one year of the first episode. This is due, in part, to damage from the first episode. The performance of a new drug designed to prevent a second episode is to be tested for its effectiveness in preventing a second episode. In order to do this two groups of people suffering a first episode are selected. There are 163 people in the first group and this group will be administered the new drug. There are 160 people in the second group and this group wil be administered a placebo. After one year, 13% of the first group has a second episode and 14% of the second group has a second episode. Select a 90% confidence interval for the difference in true proportion of the two groups.

a) [0.00590, 0.0251].
b) [0.00690, 0.0551].
c) [0.0890, 0.0551].
d) [0.00690, 0.0351].
e) [0.00890, 0.0651].

Answer 1

90% confidence interval for the difference in true proportion of the two groups is (-0.0717, 0.0517).

Explanation:

Before building the confidence interval, we need to understand the central limit theorem and subtraction of normal variables.

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

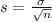For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
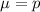`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

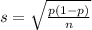
Subtraction between normal variables:

When two normal variables are subtracted, the mean is the difference of the means, while the standard deviation is the square root of the sum of the variances.

First group: Sample of 163, 13% has a second episode.

This means that:

`p_1 = 0.13, s_1 = \sqrt{(0.13*0.87)/(163)} = 0.026`

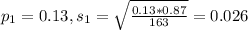
Second group: Sample of 160, 14% has a second episode

This means that:

`p_2 = 0.14, s_2 = \sqrt{(0.14*0.86)/(160)} = 0.027`

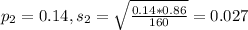
Distribution of the difference:

`p = p_1 - p_2 = 0.13 - 0.14 = -0.01`

`s = √(s_1^2+s_2^2) = √(0.026^2+0.027^2) = 0.0375`

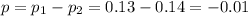
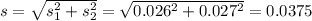
Confidence interval:

The confidence interval is:

`p \pm zs`

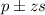
In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`.

90% confidence level

So
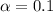`\alpha = 0.1`, z is the value of Z that has a pvalue of
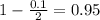`1 - (0.1)/(2) = 0.95`, so
`Z = 1.645`.

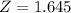Lower bound:

`p - 1.645s = -0.01 - 1.645*0.0375 = -0.0717`

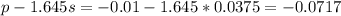
Upper bound:

`p + 1.645s = -0.01 + 1.645*0.0375 = 0.0517`

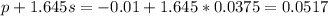
90% confidence interval for the difference in true proportion of the two groups is (-0.0717, 0.0517).