Answer:
Hence, the relation R is a reflexive, symmetric and transitive relation.
Given :
A be the set of all lines in the plane and R is a relation on set A.
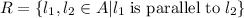
To find :
Which type of relation R on set A.
Explanation :
A relation R on a set A is called reflexive relation if every
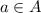 then
then
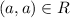 .
.
So, the relation R is a reflexive relation because a line always parallels to itself.
A relation R on a set A is called Symmetric relation if
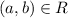 then
then
 for all
for all
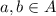 .
.
So, the relation R is a symmetric relation because if a line
 is parallel to the line
is parallel to the line
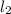 the always the line
the always the line
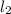 is parallel to the line
is parallel to the line
 .
.
A relation R on a set A is called transitive relation if
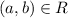 and
and
 then
then
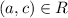 for all
for all
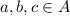 .
.
So, the relation R is a transitive relation because if a line
 s parallel to the line
s parallel to the line
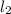 and the line
and the line
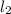 is parallel to the line
is parallel to the line
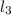 then the always line
then the always line
 is parallel to the line
is parallel to the line
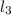 .
.
Therefore the relation R is a reflexive, symmetric and transitive relation.