Answer:
0.2097 = 20.97% probability that your longest wait is less than 12 minutes
Explanation:
To solve this question, we need to understand the uniform and the binomial distribution.
Uniform distribution:
A distribution is called uniform if each outcome has the same probability of happening.
The uniform distribution has two bounds, a and b, and the probability of finding a value lower than x is given by:
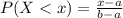
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

And p is the probability of X happening.
Probability of a single bus having a waiting time of less than 12 times:
Uniformly distributed on the interval [0, 15] means that

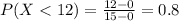
What is the probability that your longest wait is less than 12 minutes?
This is the probability that all 7 buses have waiting time less than 12 minutes, which is
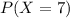 when
when
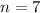 , with
, with
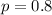 . So
. So

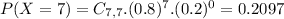
0.2097 = 20.97% probability that your longest wait is less than 12 minutes