Question

Some rectangles have an area of 36 cm². Let the variable W represent the width of these rectangles. Which expression represents the perimeters of these rectangles?

Answer 1

The perimeter of the rectangle is expressed as;
`P = (72 \ + \ 2W^2)/(W)`

Explanation:

Given;

area of the rectangle, A = 36 cm²

width of the rectangle, = W

Let L represent the length of the rectangle,

A = L x W

`L = (A)/(W) = (36)/(W)`

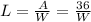
The perimeter of the rectangle is calculated as;

P = 2(L + W)

Substitute the value of L into the above equation;

`P = 2(L + W)\\\\P = 2 ((36)/(W) + W)\\\\P = 2 ((36 + W^2)/(W) )\\\\P = (72 \ + \ 2W^2)/(W)`

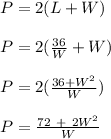
Thus, the perimeter of the rectangle is expressed as
`P = (72 \ + \ 2W^2)/(W)`