Question

Find the measure of side c. Triangle A B C has a right angle at angle C. The measure of angle A is 29 degrees. Hypotenuse A B is labeled "c" and leg B C is labeled "a = 33 meters." 29 o c a = 33 m

Answer 1

Given:

In triangle ABC, right angle at angle C.

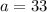`a = 33` meters

`m\angle A=29^\circ`

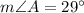
To find:

The measure of side c.

Solution:

In a right angle triangle,

`\sin \theta =(Perpendicular)/(Hypotenuse)`

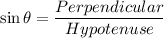
It is also written as:

`\sin \theta =(Opposite)/(Hypotenuse)`

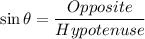
In triangle ABC, angle C is a right angle. It means the side c is the hypotenuse.

In triangle ABC,

`\sin A=(a)/(c)`

`\sin 29^\circ=(33)/(c)`

`c=(33)/(\sin 29^\circ)`

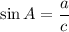
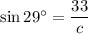
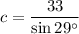
On further simplification, we get

`c=(33)/(0.4848)`

`c=68.0693`

`c\approx 68.07`

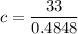
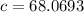
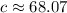
Therefore, the measure of side c is 68.07 meters.