Question

When n=343 college students are randomly selected and surveyed, it is found that x=110 own a car. Find a 99% confidence interval (CI) and margin of error (ME) for the true proportion of all college students who own a car.

Answer 1

The margin of error will be "0.65". A further explanation is provided below.

Explanation:

The given values are:

n = 343

x = 110

At 99% confidence level,

`\alpha = 1-99`%

`=1-0.99`

`=0.01`

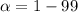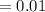
then,

`(\alpha)/(2) =(0.01)/(2)`

`=0.005`

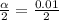
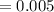
or,

`Z_{(\alpha)/(2) }=Z_(0.005)`

`=2.576`

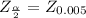
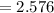
Now,

The point estimate will be:

⇒
`\hat{P}=(x)/(n)`

⇒
`=(110)/(343)`

⇒
`=0.321`

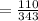
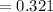
or,

⇒
`1-\hat{P}=1-0.321`

⇒
`=0.679`

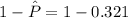
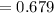
The margin of error will be:

⇒
`E=Z_{(\alpha)/(2) }* \sqrt (\frac{(\hat{P}* (1 - \hat{P})) }{n} )`

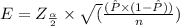
On substituting the above values, we get

⇒
`=2.576* \sqrt{(0.321* 0.679)/(343) }`

⇒
`=2.576* \sqrt{(0.217959)/(343) }`

⇒
`=0.065`

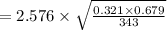
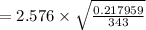
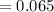
hence,

⇒
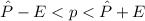
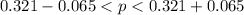
`\hat{P}-E<p<\hat{P}+E`

⇒
`0.321-0.065<p<0.321+0.065`

⇒
`0.256,0.386`