Answer:
The p-value of the test is 0.0207.
Explanation:
Test of the claim that more than 60% of the people following a particular diet will experience increased energy (H1: p > 0.6).
The null hypothesis is:
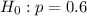
The alternate hypothesis is:
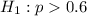
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
0.6 is tested at the null hypothesis:
This means that
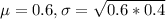
Of 100 randomly selected subjects who followed the diet, 70 noticed an increase in their energy level.
This means that
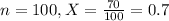
Test statistic:

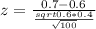
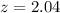
P-value of the test:
The p-value of the test is the probability of finding a sample proportion of at least 0.7, which is 1 subtracted by the p-value of z = 2.04.
Looking at the z-table, z = 2.04 has a p-value of 0.9793
1 - 0.9793 = 0.0207
The p-value of the test is 0.0207.