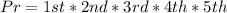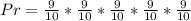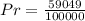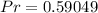Answer:
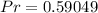
Explanation:
See Comment for Complete Question
Given that A has 5 digits. A digit in A can be chosen from 0 to 9 (10 digits).
However, selection without 4 means that we can only select from 0 to 3 and 5 to 9 (altogether, that is 9 digits)
The probability of selecting a number other than 4 in each of the digit is:
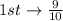
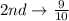
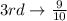
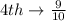
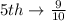
So, the required probability is: