Answer:
a) The coordinates of the rest stop is
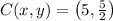 .
.
b) The approximate distance between the high school and the stadium is 32 miles.
Explanation:
a) The rest stop is located in the midpoint of the line segment between the high school and the stadium. Vectorially speaking, we use the following formula:
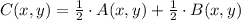 (1)
(1)
Where:
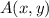 - Coordinates of the high school.
- Coordinates of the high school.
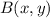 - Coordinates of the stadium.
- Coordinates of the stadium.
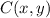 - Coordinates of the rest stop.
- Coordinates of the rest stop.
If we know that
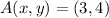 and
and
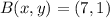 , then the coordinates of the rest stop are, respectively:
, then the coordinates of the rest stop are, respectively:
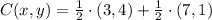

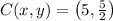
The coordinates of the rest stop is
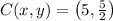 .
.
b) The approximate distance between the high school and the stadium (
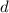 ), in miles, is the product of the Length Equation of the Line Segment and the scale factor:
), in miles, is the product of the Length Equation of the Line Segment and the scale factor:
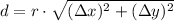 (2)
(2)
Where:
 - Scale factor, in miles.
- Scale factor, in miles.
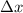 ,
,
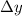 - Horizontal and vertical distances between the high school and the stadium, no unit.
- Horizontal and vertical distances between the high school and the stadium, no unit.
If we know that
 ,
,
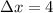 and
and
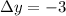 , then the distance between the high school and the stadium is:
, then the distance between the high school and the stadium is:
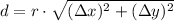
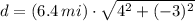

The approximate distance between the high school and the stadium is 32 miles.