Question

Ou are trying to estimate the average amount a family spends on food during a year. In the past, the standard deviation of the amount a family has spent on food during a year has been σ = $1200. If you want to be 99% sure that you have estimated average family food expenditures within $60, how many families do you need to survey? Place your answer, a whole number, do not use any decimals, in the blank___.

Answer 1

The answer is "2653".

Explanation:

`Sample \ Size = 99\% \ Cl\\\\ E =60 \\\\\sigma= 1200\\\\`

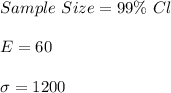
Minimum sample size for Cl level
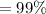`= 99\%` and Desired Margin of Error,
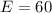`E = 60` is:

`\to P(|\bar{x}-\mu| < E) \geq 1-\alpha \\\\\to P(\frac{\bar{x}-\mu}{(\sigma)/(√(n))} <- (E)/((\sigma)/(√(n)))) \leq (\alpha)/(2) \\\\\to - (E)/((\sigma)/(√(n))) \leq -z_{(\alpha)/(2)} \\\\\to n\geq (\frac{ z_{(\alpha)/(2) * \alpha} }{E})^2 \\\\`

`Margin \ Error = \frac{\text{length of the CI}}{2}\\\\\sigma=1200\\\\\alpha=1 - Confidence =1-0.99=0.01\\\\Z_{(\alpha)/(2)}=z_(0.005)=2.58\\\\n\geq ((z_(0.005) * \sigma )/(E))^2 \\\\= ((2.58 * 1200 )/(60))^2\\\\=2662.560\\`

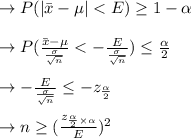
The minimum n has to be integer, we take the ceiling Of above number and get n = 2663

The exact z-value.

`n \geq ((2.5758293035489 * 1200)/(60))^2 \\\\= 2653.95864`

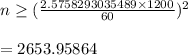
using critical value of 2,575, which gives 2652.25

`\to n =2653`