Question

Why do you sometimes finish the square (ex.
`x^(2) + 4x=1`) and sometimes you make one side zero(ex
`x^(2) -12x=-35`)? How should I know the difference? Any help is appreciated! TIA

Answer 1

I'm assuming we're asking about the difference between:

`ax^2 + bx + c = 0`

and

`ax^2 + bx = -c`

Let's preface this by stating the obvious: there's no actual difference. Both equations are equivalent.

Now, it has a lot to do with our goal. Sometimes our goal is to write an equation concisely (then the "no-zero" way uses less characters), and sometimes we're dealing with a quadratic function of

`y = ax^2 + bx + c`

in the second case, we wouldn't write

`y - c = ax^2 + bx`

because it'd be confusing. That means that when we're looking for y=0 points of a quadratic equation, the way to convey that goal is that we're looking for the point where
`ax^2 + bx + c = 0` - so we preserve the structure of the quadratic function.

Answer 2

Lets say there's a quadratic equation → ax² + bx = -c

Lets make one side zero which gives → ax² + bx + c = 0

From the above equation ,

• if you can split b into 'p' & 'q' (some real numbers) such that p + q = b & pq = ac ; then the quadratic equation can be easily solved by using factorisation method. Here the easiest way to guess the values of 'p' & 'q' is to find out the prime factors of 'ac' and taking any two prime numbers in random , just check whether the sum of those two primes is equal to 'b' (excluding their signs).

• if you can't split b into 'p' & 'q' (some real numbers) such that p + q = b & pq = ac ; then try solving quadratic equation by completing the squares method.

For example :- x² - 12x = -35.

Lets make one side zero → x² - 12x + 35 = 0 . Now, lets break -12x into two real numbers 'p' & 'q' such that p + q = -12x & pq = 35. Prime factors of 35 are 1 , 5 & 7. If we take 5 & 7 as 'p' & 'q' then p + q = 5 + 7 = 12. but as we need -12 , the values of 'p' & 'q' are -5 & -7.

⇒
`x^2 -5x - 7x + 35 = 0`

⇒
`x(x - 5) - 7(x - 5) = 0`

⇒
`(x - 5)(x - 7) = 0`

⇒
`x = 5 \: or \: 7`

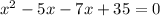
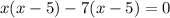
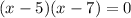
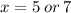
Lets take another example :- x² + 4x = 1.

Lets make one side zero → x² + 4x - 1 = 0 . Now , lets split +4x into into two real numbers 'p' & 'q' such that p + q = +4x & pq = -1 . Prime factors of 4 are 1 & 2 only. But there's no such combination of its primes such that their sum would be equal to 4. So, the quadratic equation can't be solved by factorisation method. Now, lets bring -1 to Right Hand Side & try solving by completing squares method.

⇒
`x^2 + 2 * x * 2 + 2^2 = 1 + 2^2`

⇒
`(x + 2)^2 = 1 + 4 = 5`

⇒
`x + 2 = +√(5) \: \: or \: -√(5)`

⇒
`x = (√(5) - 2) \: or \: (-√(5) -2)`

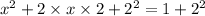
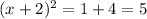
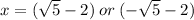
Conclusion:

First try making one side zero and try to solve the equation by factorisation method. If it got factorised , then you are done and if it didn't get factorised , then solve it by completing squares method.