Question

The area of a rectangle is (81x2 − 4y2) square units. Determine the dimensions of the rectangle by factoring the area expression completely. Show your work. (5 points)

Answer 1

(9x + 2y)(9x - 2y)

Explanation:

The rule: a^2 - b^2 = (a + b)(a - b)

81x^2 - 4y^2

And we have a = 9x and b = 2y

and our factors are.

(9x + 2y)(9x - 2y)

so the the dimensions are 9x + 2y and 9x - 2y

hope this helps

~~~Wdfads~~~

Answer 2

The dimension of the rectangle are
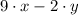`9\cdot x - 2\cdot y` units and
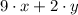`9\cdot x + 2\cdot y` units, respectively.

Explanation:

Geometrically speaking, the area of a rectangle is equal to the product of its base and its height. If we know that area of the figure is
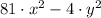`81\cdot x^(2) - 4\cdot y^(2)` square units, then we proceed to factor the expression:

1)
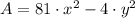`A = 81\cdot x^(2) - 4\cdot y^(2)` Given

2)
`A = (9\cdot x -2\cdot y)\cdot (9\cdot x + 2\cdot y)`
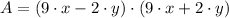
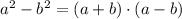`a^(2) - b^(2) = (a + b) \cdot (a - b)`/Result

The dimension of the rectangle are
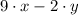`9\cdot x - 2\cdot y` units and
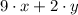`9\cdot x + 2\cdot y` units, respectively.