Question

Quadratics need help making parabola

Answer 1

The equation of the parabola is
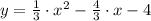`y = (1)/(3)\cdot x^(2)-(4)/(3)\cdot x -4`, whose real vertex is
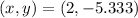`(x,y) = (2, -5.333)`, not
`(x,y) = (2, -5)`.

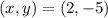Explanation:

A parabola is a second order polynomial. By Fundamental Theorem of Algebra we know that a second order polynomial can be formed when three distinct points are known. From statement we have the following information:

`(x_(1), y_(1)) = (-2, 0)`,
`(x_(2), y_(2)) = (6, 0)`,
`(x_(3), y_(3)) = (0, -4)`

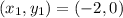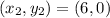From definition of second order polynomial and the three points described above, we have the following system of linear equations:

`4\cdot a -2\cdot b + c = 0` (1)

`36\cdot a + 6\cdot b + c = 0` (2)

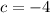`c = -4` (3)

The solution of this system is:
`a = (1)/(3)`,
`b = - (4)/(3)`,
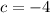`c = -4`. Hence, the equation of the parabola is
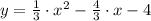`y = (1)/(3)\cdot x^(2)-(4)/(3)\cdot x -4`. Lastly, we must check if
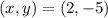`(x,y) = (2, -5)` belongs to the function. If we know that
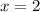`x = 2`, then the value of
`y` is:

`y = (1)/(3)\cdot (2)^(2)-(4)/(3)\cdot (2) - 4`

`y = -5.333`

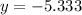
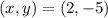`(x,y) = (2, -5)` does not belong to the function, the real point is
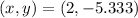`(x,y) = (2, -5.333)`.