Question

Find the volume and surface area of the composite figure. Give your answer in terms of pi

PLS HELP

Answer 1

Given:

A diagram of a composite figure.

Radius of cone and hemisphere is 8 cm.

Height of the cone is 15 cm.

To find:

The volume and the surface area of the composite figure.

Solution:

Volume of a cone is:

`V_1=(1)/(3)\pi r^2h`

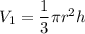
Where, r is the radius and h is the height of the cone.

Putting
`r=8,h=15` in the above formula, we get

`V_1=(1)/(3)\pi (8)^2(15)`

`V_1=\pi (64)(5)`

`V_1=320\pi`

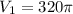
Volume of the hemisphere is:

`V_2=(2)/(3)\pi r^3`

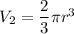
Where, r is the radius.

Putting
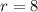`r=8`, we get

`V_2=(2)/(3)\pi (8)^3`

`V_2=(1024)/(3)\pi`

`V_2\approx 341.3\pi`

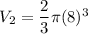
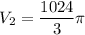
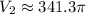
Now, the volume of the composite figure is:

`V=V_1+V_2`

`V=320\pi +341.3\pi`

`V=661.3\pi`

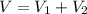
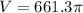
The volume of the composite figure is 661.3π cm³.

The curved surface area of a cone is:

`A_1=\pi r√(h^2+r^2)`

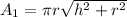
Where, r is the radius and h is the height of the cone.

Putting
`r=8,h=15` in the above formula, we get

`A_1=\pi (8)√((15)^2+(8)^2)`

`A_1=\pi (8)√(289)`

`A_1=\pi (8)(17)`

`A_1=136 \pi`

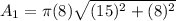
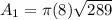
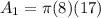
The curved surface area of the hemisphere is:

`A_2=2\pi r^2`

Where, r is the radius.

Putting
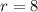`r=8`, we get

`A_2=2\pi (8)^2`

`A_2=2\pi (64)`

`A_2=128\pi`

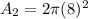
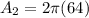
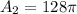
Total surface area of the composite figure is:

`A=A_1+A_2`

`A=136\pi +128\pi`

`A=264\pi`

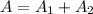
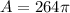
The total surface area of the composite figure is 264π cm².

Therefore, the correct option is A.