Question

Find a positive angle less than 360° that is coterminal with the given angle.

- 215°
A positive angle less than 360° that is coterminal with - 215° is

Answer 1

The positive angle less than 360° that is coterminal with -215° has a measure of 145°.

Explanation:

From Geometry, we know that angles form a family of coterminal angles as function of number of revolutions done on original angle. We can represent the set of all coterminal angles by means of the following expression:

`\theta_(c) = \theta_(o) + 360\cdot i`,
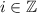`i \in \mathbb{Z}` (1)

Where:

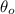`\theta_(o)` - Original angle, in sexagesimal degrees.

`\theta_(c)` - Coterminal angle, in sexagesimal degrees.

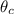`i` - Coterminal angle index, no unit.

If we know that
`\theta_(o) = -215^(\circ)` and
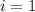`i = 1`, then the coterminal angle that is less than 360° is:

`\theta_(c) = -215^(\circ) + 360\cdot (1)`

`\theta_(c) = 145^(\circ)`

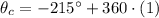
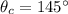
The positive angle less than 360° that is coterminal with -215° has a measure of 145°.