Answer:
P(Hispanic or Bilingual) = 0.429.
Explanation:
This question is solved treating these events as Venn probabilities.
I am going to say that:
Event A: Hispanic
Event B: Bilingual
Out of 14 teachers, 4 are Hispanic, 5 are billingual, and 3 are both:
This means that:
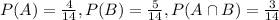
What is the probability that teacher is Hispanic or bilingual?
This is:
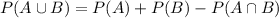
With the values that the exercise gives us:
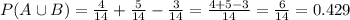
So
P(Hispanic or Bilingual) = 0.429.