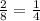Question

7. Murray spins the pointer of the spinner shown at the right

a. What is the sample space for the probability model?
b. What is the probability of each event in the sample space?

Answer 1

a)

Sample Space of Probability model is - S' = {
`(1)/(4)` ,
`(1)/(4)` ,
`(1)/(4)` ,
`(1)/(4)` }

b)

Probability of Event 1 , P(1) =
`(2)/(8) = (1)/(4)`

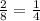
Probability of Event 2 , P(2) =
`(2)/(8) = (1)/(4)`

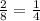
Probability of Event 3 , P(3) =
`(2)/(8) = (1)/(4)`

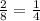
Probability of Event 4 , P(4) =
`(2)/(8) = (1)/(4)`

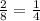
Explanation:

Given - Murray spins the pointer of the spinner as shown .

To find - a. What is the sample space for the probability model?

b. What is the probability of each event in the sample space?

Proof -

The Sample space is the set of all possible outcomes.

So,

Sample space becomes -

S = { 3, 5, A, Y, 3, 5, A, Y}

Total number of outcomes, n(S) = 8

Now,

We can see that There are 4 types of event

Event 1 : 3

Event 2 : 5

Event 3 : A

Event 4 : Y

So,

Probability of Event 1 , P(1) =
`(2)/(8) = (1)/(4)`

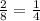
Probability of Event 2 , P(2) =
`(2)/(8) = (1)/(4)`

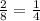
Probability of Event 3 , P(3) =
`(2)/(8) = (1)/(4)`

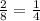
Probability of Event 4 , P(4) =
`(2)/(8) = (1)/(4)`

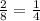
Now,

Sample Space of Probability model is -

S' = {
`(1)/(4)` ,
`(1)/(4)` ,
`(1)/(4)` ,
`(1)/(4)` }

∴ we get

a)

Sample Space of Probability model is - S' = {
`(1)/(4)` ,
`(1)/(4)` ,
`(1)/(4)` ,
`(1)/(4)` }

b)

Probability of Event 1 , P(1) =
`(2)/(8) = (1)/(4)`

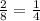
Probability of Event 2 , P(2) =
`(2)/(8) = (1)/(4)`

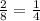
Probability of Event 3 , P(3) =
`(2)/(8) = (1)/(4)`

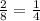
Probability of Event 4 , P(4) =
`(2)/(8) = (1)/(4)`