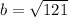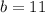Question

Find the missing side lengths. Leave your answers as radicals in simplest form.

Sep by step explanation pls​

Answer 1

`a =22`

`b = 11`

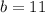
Explanation:

Given

See attachment for triangle

Required

Find a and b

Using cosine formula, we have:

`\cos \theta = (Adjacent)/(Hypotenuse)`

So, we have:

`\cos (30) = (11\sqrt 3)/(a)`

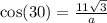
Make a the subject

`a = (11\sqrt 3)/(\cos (30))`

`\cos(30) = (\sqrt 3)/(2)`

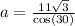
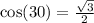
So, we have:

`a = (11\sqrt 3)/((\sqrt 3)/(2))`

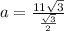
Rewrite as:

`a = 11\sqrt 3 / (\sqrt 3)/(2)`

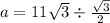
This gives:

`a = 11\sqrt 3 * (2)/(\sqrt 3)`

`a = 11 * 2`

`a =22`

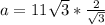
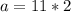
To solve for b, we use Pythagoras theorem

`a^2 = b^2 + (11\sqrt 3)^2`

`22^2 = b^2 + (11\sqrt 3)^2`

`484 = b^2 + 363`

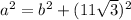
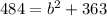
Collect like terms

`b^2 = 484 - 363`

`b^2 = 121`

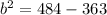
Take positive square roots

`b = \sqrt {121`

`b = 11`