Question

Describe the behavior of the function p around its vertical asymptote at x = -9

Answer 1

Explanation:

The graph of P approaches -∞from the left and +∞ from the right of the asymptote

Answer 2

The correct option is:

"The graph of p approaches
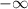`\( -\infty \)` from the left and
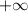`\( +\infty \)` from the right of the asymptote."

To describe the behavior of the function
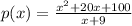`\( p(x) = (x^2 + 20x + 100)/(x + 9) \)`around its vertical asymptote at x = -9 , we need to look at the limits of p(x) as x approaches -9 from the left and from the right:

1. The limit of p(x) as x approaches -9 from the left
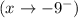`(\( x \to -9^- \))` is
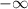`\( -\infty \)`. This means that as x gets closer to -9 from values less than -9, p(x) decreases without bound.

2. The limit of p(x) as x approaches -9 from the right
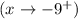`(\( x \to -9^+ \))` is
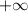`\( +\infty \)`. This means that as x gets closer to -9 from values greater than -9, p(x) increases without bound.

So the behavior of the function p around its vertical asymptote at x = -9 is:

- The graph of p approaches
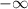`\( -\infty \)` from the left of the asymptote.

- The graph of p approaches
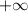`\( +\infty \)` from the right of the asymptote.