Question

A population of rabbits in a lab, r(x), can be modeled by the function r(x) = 30(1.02)^x, where x represents the number of days since the population was first counted. Determine, to the nearest tenth, the average rate of change from day 35 to 52, including units

Answer 1

The population of the rabbits in the lab grew, on average, at a rate of 1.4 rabbits per day from day 35 to 52.

Explanation:

The average rate of change of a function between two points is essentially the slope between them.

We have the function:

`r(x)=30(1.02)^x`

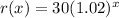
And we want to find the average rate of change from x = 35 to x = 52.

We can use the slope formula:

`\displaystyle m=(y_2-y_1)/(x_2-x_1)`

Our first point will be (35, r(35)) and our second point is (52, r(52)). Substitute:

`\displaystyle m=(r(52)-r(35))/(52-35)`

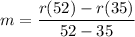
Note that our outputs y are rabbits and our inputs or x are days. Substitute:

`\displaystyle m=\frac{30(1.02)^(52)-30(1.02)^(35) \text{ rabbits}}{52-35\text{ days}}`

Use a calculator:

`\displaystyle m\approx\frac{1.4\text{ rabbits}}{\text{day}}`

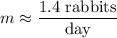
So, the population of the rabbits in the lab grew on average at a rate of 1.4 rabbits per day from day 35 to 52.