Question

Can someone please help me with this?

Answer 1

Answer: The last option has no solution.

1. ) The solution is 1/2

2) The solution is -17/27

3) The solution is infinitely many solutions.

4) There is no solution because the answer solved and simplified comes out to be 17= -10; this is impossible so there is no solution

Answer 2

5(2.2y + 3.4) = 5(y - 2) + 6y

Explanation:

In order to answer this question, one must solve each of the equations until one has reached a conclusion that the parameter (y) has no solution in the given circumstance.

Equation 1

13y + 2 - 2y = 10y + 3 - y

Simplify, combine like terms;

11y + 2 = 9y + 3

Inverse operations,

11y + 2 = 9y + 3

-9y

2y + 2 = 3

-2

2y = 1

/2

y = 0.5

Equation 2

9(3y + 7) - 2 = 3(-9y + 9)

Distribute, multiply every term inside the parenthesis by the term outside of it;

(9)(3y) + (9)(7) - 2 = (3)(-9y) + (3)(9)

Simplify,

27y + 63 - 2 = -27y + 27

27y + 61 = -27y + 27

Inverse operations,

27y + 61 = -27y + 27

+27y

54y + 61 = 27

-61

54y = 34

/54

y =
`(17)/(27)`

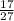
Equation 3

32.1y + 3.1 + 2.4y - 8.2 = 34.5y - 5.1

Simplify, combine like terms;

34.5y - 5.1 = 34.5y - 51

As one can see, this equation is an identity, meaning that any value can be substituted into the parameter (y) to produce a true result.

Equation 4

5(2.2y + 3.4) = 5(y - 2) + 6y

Distribute, multiply every term in the parenthesis by the term outside of it;

(5)(2.2y) + (5)(3.4) = (5)(y) + (5)(-2) + 6y

Simplify,

11y + 17 = 5y - 10 + 6y

11y + 17 = 11y - 10

Inverse operations,

11y + 17 = 11y - 10

-11y

17 = -10

One can see that this equation produces a false result since it is common knowledge that (17) cannot equal (-10). Therefore, this equation has no solutions.