Answer:
Length = (x + 8) ft
Explanation:
We are given the floor plan of a rectangular room, with the following dimensions:
Area (A) = (x² + 14x + 48) ft²
Width (W) = (x + 6) ft
Length (L) = unknown
We also know that the formula for finding the area of a rectangle is:
A = L × W
We can rearrange the formula to isolate the length by dividing both sides of the equation by W:
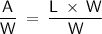
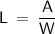
Find the factors of x² + 14x + 48:
Next, we must find the factors of the given area of a rectangle. We can do so by using the factoring by grouping method:
ax² + bx + c ⇒ (ax² + mx)(nx + c)
a = 1, b = 14, c = 48
In order to do so, we must find factors for "m" and "n," such that:
The product of m × n = 48, and
The sum of m + n = 14.
The possible factors that have a product of 48 and a sum of 14 are 6 and 8. Therefore:
m = 6 and n = 8.
= (x² + 6x) + (8x + 48)
Next, factor out x from the first group:
= x(x + 6) + (8x + 48)
Then, factor out 8 from the second group:
= x(x + 6) + 8(x + 6)
Finally, factor out the common term between both groups, (x + 6). Then, combine x + 8:
= x(x + 6) + 8(x + 6)
x² + 14x + 48 = (x + 6)(x + 8)
Solve for the Length of the Rectangle:
Now that we have our factors for the given Area of a rectangle, we can proceed with finding the length of the floor plan. Substitute the values into the following formula:
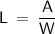
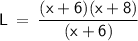 ⇒ (x + 6) cancels out, leaving us with (x + 8):
⇒ (x + 6) cancels out, leaving us with (x + 8):
L = x + 8
Double-check:
Area (A) = (x² + 14x + 48) ft²
Width (W) = (x + 6) ft
Length (L) = (x + 8) ft
In order to verify whether we have the correct value for the length, substitute its value into the formula for finding the area of a rectangle:
A = L × W
x² + 14x + 48 = (x + 8)(x + 6)
Perform the FOIL method on the right-hand side of the equation:
x² + 14x + 48 = x² + 6x + 8x + 48
Combine like terms on the right-hand side:
x² + 14x + 48 = x² + 14x + 48 ⇒ True statement.
Final answer:
Therefore, the length of the floor plan is (x + 8) ft.