Question

Determine the coordinates of the vertex for each quadratic function and whether the parabola has a maximum or minimum. 4. y = x² +6x-2​

Answer 1

vertex = (-3, -11)

minimum

Step-by-step explanation:

The vertex of a parabola is its turning point (stationary point).

Therefore, the x-coordinate of the vertex can be determined by differentiating the function, setting it zero and solving for x:

`(dy)/(dx)=2x+6`

`(dy)/(dx)=0\implies 2x+6=0 \implies x=-3`

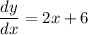
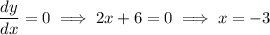
Substitute found value for x into the original function to find the y-coordinate:

`\implies (-3)^2+6(-3)-2=-11`

Therefore, the vertex is (-3, -11)

As the leading term of the quadratic function (
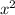`x^2`) is positive, the parabola will open upwards, so the vertex is its minimum point.

Answer 2

minimum, coordinates of vertex: (-3,-11)

Step-by-step explanation:

`\sf y =x^2 +6x-2`

x coordinates on vertex:

solving steps:

• 
  `\sf (-b)/(2a)`

• 
  `\sf (-6)/(2(1))`

• 
  `\sf -3`

Find y-coordinate on vertex:

`\sf y =x^2 +6x-2`

`\sf y =(-3)^2 +6(-3)-2`

`\sf y =-11`

`\mathrm{If}\:a < 0,\:\mathrm{then\:the\:vertex\:is\:a\:maximum\:value}`

`\mathrm{If}\:a > 0,\:\mathrm{then\:the\:vertex\:is\:a\:minimum\:value}`

coordinates: (-3,-11) thus minimum