Question

Jose desea que la puerta de su cuarto solo se pueda abrir hasta cierta posicion (ver figura). Si uno de los angulos de la abertura mide (x + 5)° y la otra (2x + 13)°. Cual seria la medida del angulo de la abertura menor?

Answer 1

La medida del ángulo de la abertura menor es 29°.

Explanation:

Podemos calcular la medida del angulo de la abertura menor hallando el valor de "x" en la siguiente ecuación:

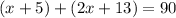`(x + 5) + (2x + 13) = 90` (1)

Dado que en la figura podemos observar que la suma de ambos ángulos de abertura resulta en un ángulo rectángulo.

Al resolver la ecuación (1) tenemos:

`x + 2x = 90 - 13 - 5`

`3x = 72`

`x = 24`

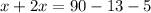
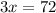
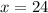
Ahora, podemos encontrar los ángulos de abertura.

Angulo de abertura menor:

`x + 5 = 24 + 5 = 29^(\circ)`

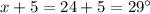
Angulo de abertura mayor:

`2x + 13 = 2*24 + 13 = 61^(\circ)`

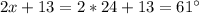
Por lo tanto, la medida del ángulo de la abertura menor es 29°.

Espero que te sea de utilidad!