Question

A person places $686 in an investment account earning an annual rate of 3.8%, compounded continuously. Using the formula V = Pe^{rt}V=Pe rt , where V is the value of the account in t years, P is the principal initially invested, e is the base of a natural logarithm, and r is the rate of interest, determine the amount of money, to the nearest cent, in the account after 15 years.

Answer 1

V = $1213.03

Explanation:

We can determine the amount of money after 15 years with the given formula:

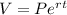`V = Pe^(rt)` (1)

Where:

V: is the value of the account in t years =?

P: is the principal initially invested = $686

r: is the rate of interest = 3.8% = 3.8/100 = 0.038

t: is the time = 15 years

By substituting the above values into equation (1) we have:

`V = Pe^(rt) = 686*e^((0.038*15)) = 1213.03`

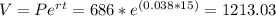
Therefore, the amount of money is $1213.03.

I hope it helps you!